PID控制
PID控制
基本概念
通过反馈系统控制某一参量时,需要通过误差来调整,而误差需要考虑三方面的因素:
- 当前的误差
- 过去的误差
- 误差的变化趋势
PID控制算法是通过比例P(Proportion)、积分I(Integral)、微分D(Differential)三种对误差的处理来实现自动控制的。
举例
调节洗澡水的温度时,通过控制水阀的旋钮来调节水温。该系统框图如下:
洗澡时有一个期望的水温,称为参考r。通过计算当前水温T与参考水温r之间的差值得到误差e。通过一个控制器,利用反馈误差e来控制旋钮角度u,进而控制水温T向参考r靠近。则有如下框图:
核心思想:通过误差e来调节输入u。
$k_{P} \cdot e$ 比例控制,$k_{P}$称为比例增益。基于当前误差。
水温较低时,调大u;水温较高时,调小u。
$k_{I} \cdot \int e dt$ 积分控制,$k_{I}$称为积分增益。基于过去误差,是一种累积。
一段时间了水温都较低,调大u;一段时间了水温都较高,调小u。
$k_{D} \cdot \frac{\mathrm{d} e}{\mathrm{d} t} $ 微分控制,$k_{D}$称为微分增益。基于误差变化趋势。
水温变化太快了,调小u;水温变化太慢了,调大u。
综合以上三项,得到u与e的关系:
$$
u = k_{P} \cdot e + k_{I} \cdot \int e dt + k_{D} \cdot \frac{\mathrm{d} e}{\mathrm{d} t}
$$
对上式两边同时做拉普拉斯变换,可以得到PID控制器的传递函数:
$$
u(s) =( k_{P} + k_{I} \cdot \frac{1}{s} + k_{D} \cdot s)E(s)
$$
将PID控制器的传递函数带入框图可得:
PID控制的simulink仿真
PD控制:提高稳定性,改善瞬态。
PI控制:改善稳态误差。
PD控制+PI控制=PID控制
仿真系统
假设有一简单二阶系统,其传递函数为:
$$
G(s)=\frac{X(s)}{U(s)}= \frac{1}{s^{2}+0.8*s+1 }
$$
初始条件为
初始条件为:$x(s)=x’(s)=0$;目标参考:$r=10$
系统框图为:
在simulink中搭建好系统如下所示:
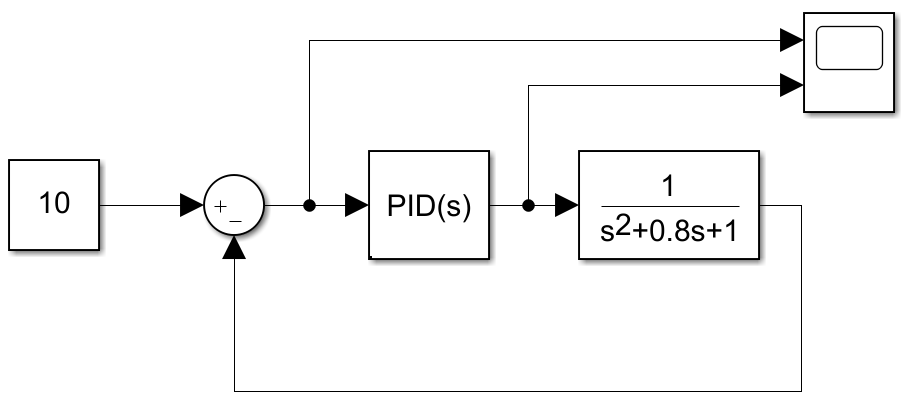
其中scope接收两路信号,分别是误差e以及经过PID控制的输入u。
不同PID参数的影响
1.P控制存在稳态误差
参数设置:$P=10,I=0,D=0$
结果:
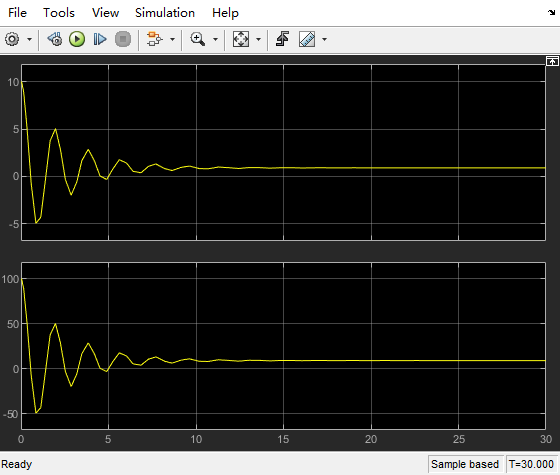
从仿真结果可以看出,误差e并没有到0,大约在1左右。说明通过比例控制是无法消除稳态误差的。
2.PI控制可以消除稳态误差
参数设置:$P=10,I=5,D=0$
结果:
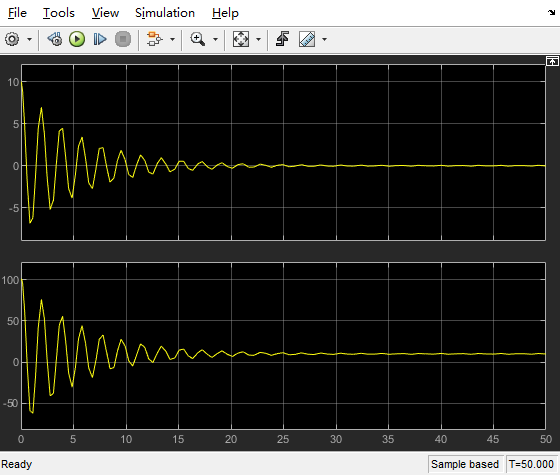
可以看到,加入积分增益后,误差e趋向于0。
3.P控制与PI控制优劣对比
下面做一个对比:
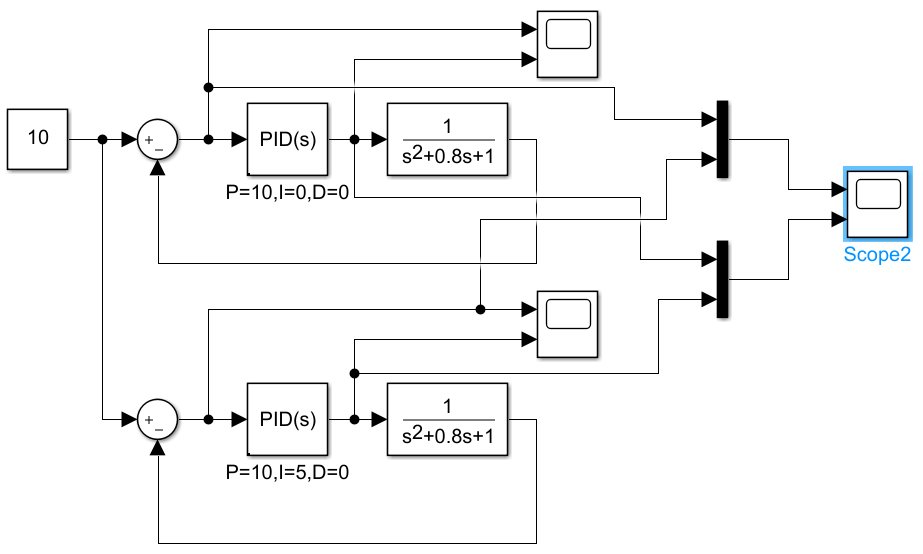
得到的结果为:
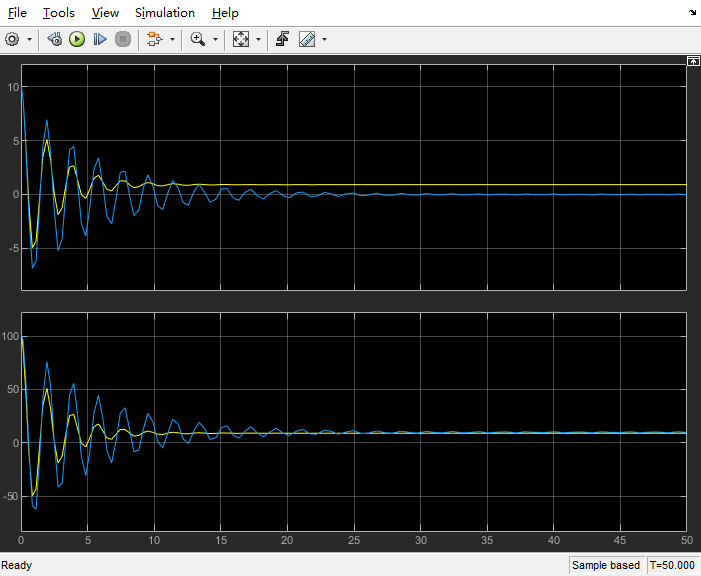
黄色为P控制,蓝色为PI控制。上面为误差e,下面为控制输入u。
可以看到,P控制的误差(上面黄色曲线)是无法达到0的,而PI控制的误差(上面蓝色曲线)可以达到0误差。虽然PI控制可以没有稳态误差,但是其振荡要比P控制强烈。黄线在T=15时即达到稳定,而蓝线直到T=30才稳定。表明PI控制达到稳定状态的时间要比P控制长。
4.PID控制
参数设置:$P=10,I=5,D=3$
结果为:
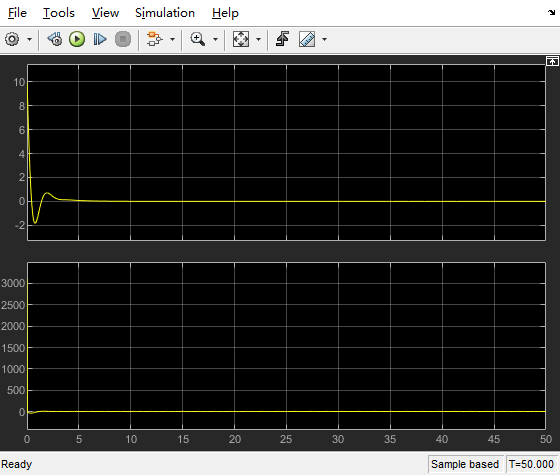
可以看出误差非常迅速的达到稳定的0值。
最终将上述三种仿真做一下对比:
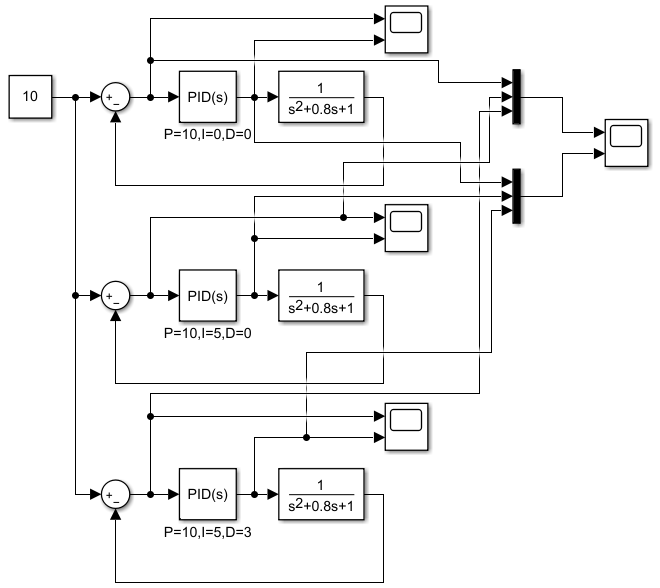
结果如下:
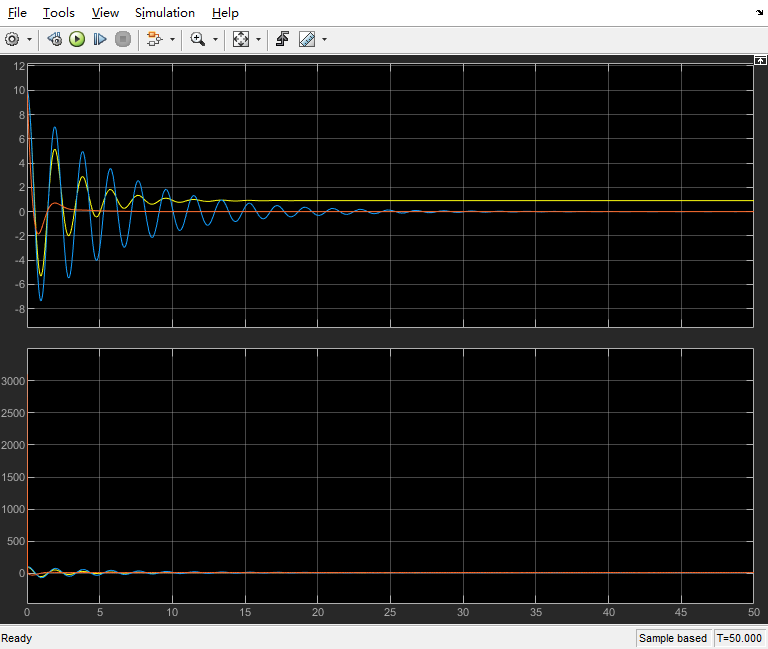
上面橙色曲线为PID控制的误差曲线。
可以看出,相较于P控制与PI控制,PID控制非常快的达到稳定的0误差,并且振荡幅度也较小。性能非常出众,但是当我们观察控制输入量u时,可以发现如下结果:
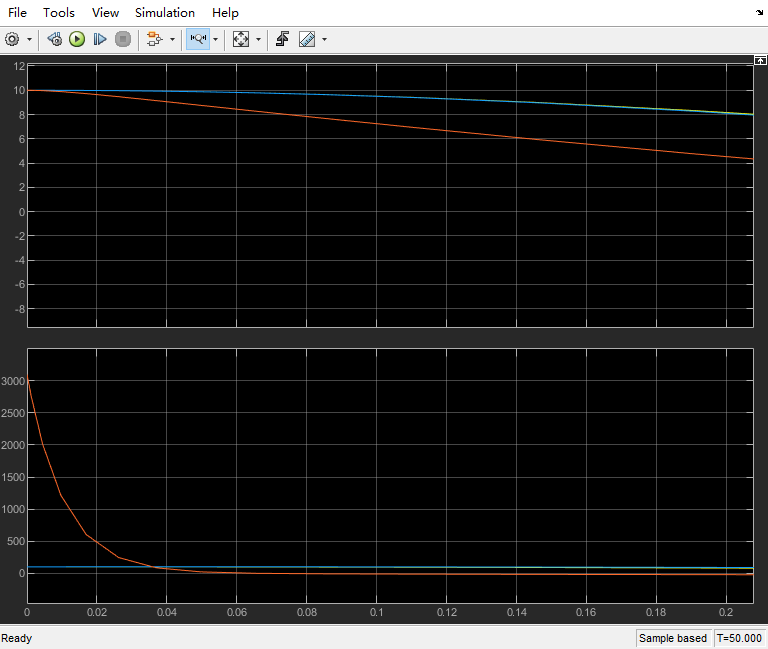
可以看出,在最开始的非常短的时间内,PID控制的输入u达到了非常高的数值,约在3000附近。而P控制以及PI控制的输入u则维持在较低的数值处。因此在实际使用中应该考虑控制器能否在初始较短时间内达到这种峰值的要求。
5.高频噪声对微分项的影响
微分项对于高频噪音非常敏感。下面做一个简单的仿真。
设置参数:噪音功率0.001,时间间隔0.01。
得到震动幅度非常小的高频噪音:
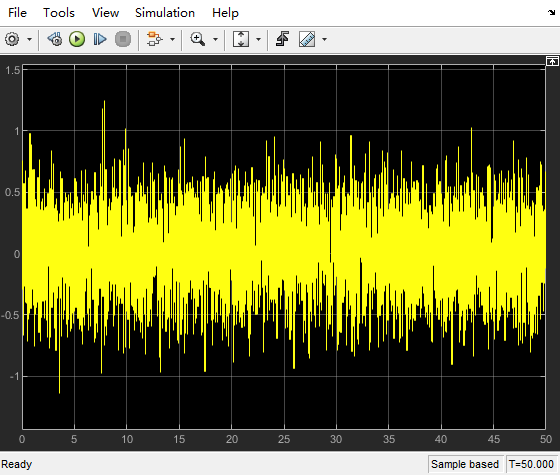
将上述噪音加入系统中:
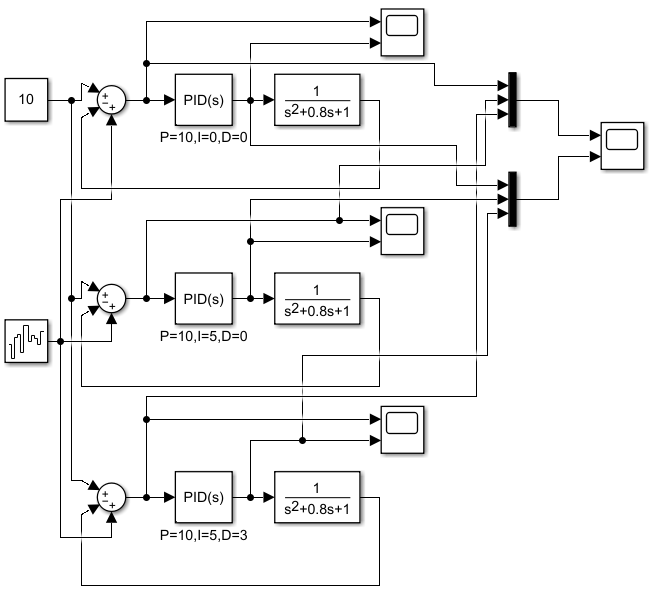
得到结果为:
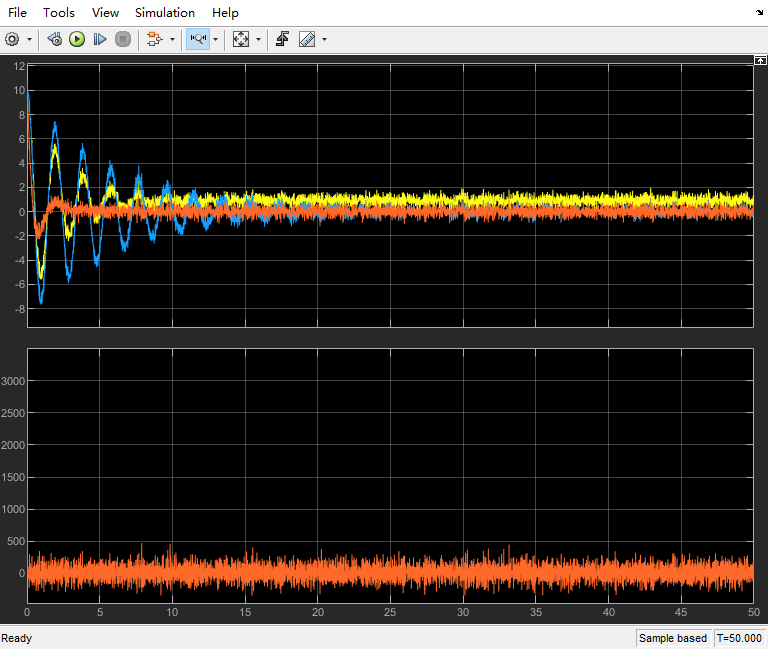
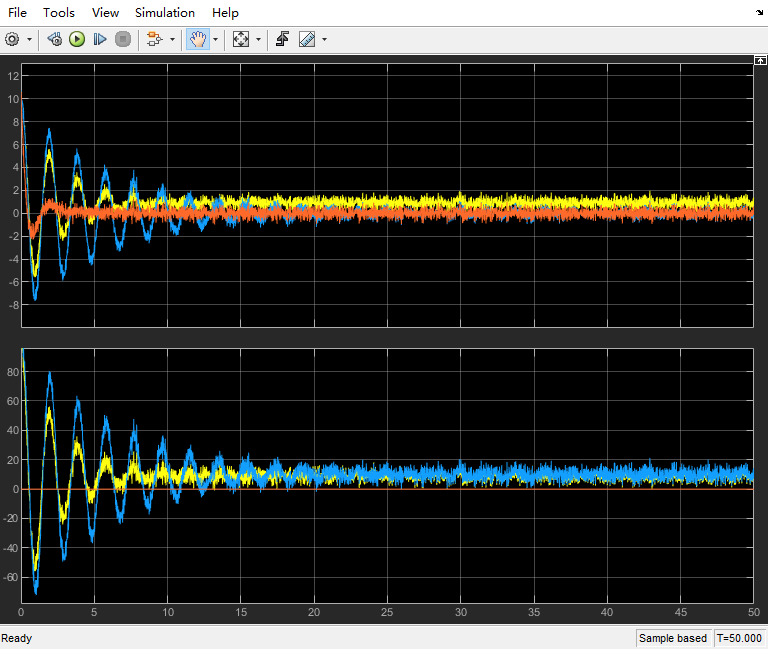
误差e(上面)存在波动,但影响不是很大。
输入u(下面)中,PID控制波动量非常大,振荡幅度在500左右,而P控制以及PI控制的波动则都在80以内。从上面的仿真中可以看出,微分项对于高频信息是非常敏感的。
微分项对于高频的敏感可以从一个简单的角度理解:
假设有一个信号$s=o.oo1*sin(1000t)$,振幅非常小但是频率非常高。对该信号进行微分$\frac{\mathrm{d} s}{\mathrm{d} t}$,结果为:$\frac{\mathrm{d} s}{\mathrm{d} t}=cos(1000t)$,振幅是原来的1000倍,这样就将频率的变化传递到了振幅的变化。因此微分项对于高频量非常敏感。
PID参数调整经验
1.手动调整

2.衰减整定
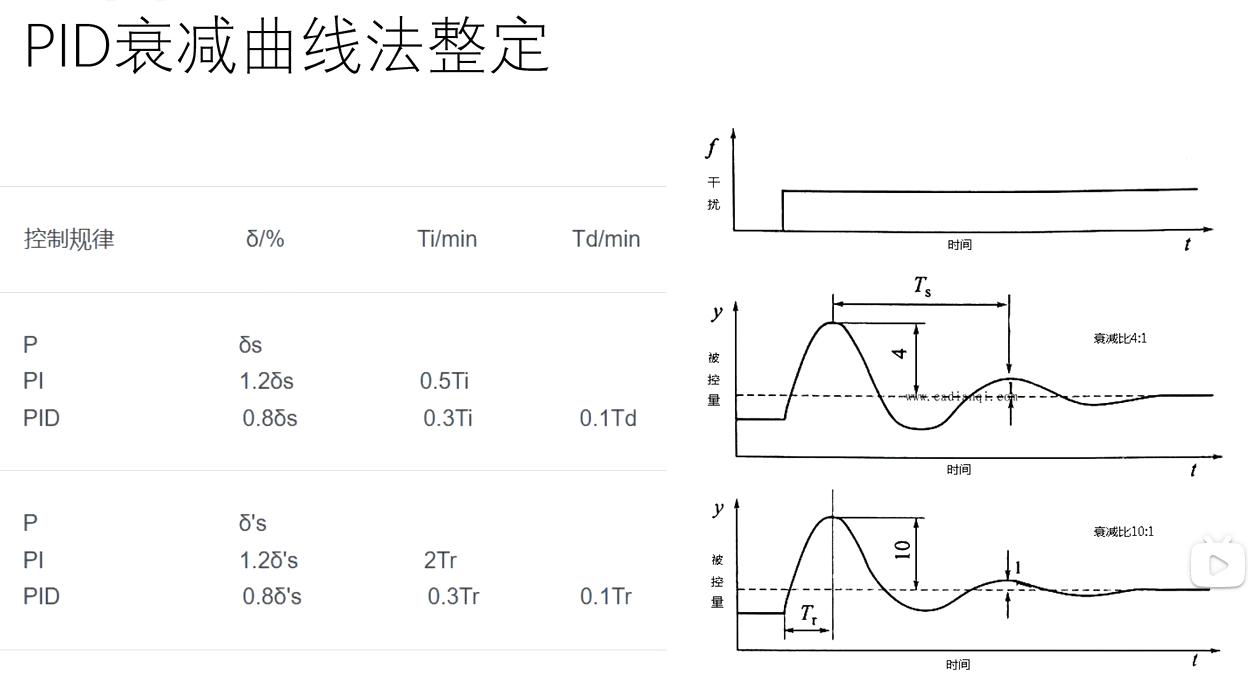
参考文献
22-7-7